Área
El área es una medida de extensión de una superficie, expresada en unidades de medida denominadas unidades de superficie. El área es un concepto métrico que requiere que el espacio donde se define se haya definido una medida.
Para superficies planas, el concepto es más intuitivo. Cualquier superficie plana de lados rectos, por ejemplo un polígono, puede triangularse y se puede calcular su área como suma de las áreas de dichos triángulos. Ocasionalmente se usa el término "área" como sinónimo de superficie, cuando no existe confusión entre el concepto geométrico en sí mismo (superficie) y la magnitud métrica asociada al concepto geométrico (área).
Sin embargo, para calcular el área de superficies curvas se requiere introducir métodos de geometría diferencial.
Para poder definir el área de una superficie en general –que es un concepto métrico–, se tiene que haber definido un tensor métrico sobre la superficie en cuestión: cuando la superficie está dentro de un espacio euclídeo, la superficie hereda una estructura métrica natural inducida por la métrica euclidiana.

Historia
La idea de que el área es la medida que proporciona el tamaño de la región encerrada en una figura geométrica proviene de la antigüedad. En el Antiguo Egipto, tras la crecida anual de río Nilo inundando los campos, surge la necesidad de calcular el área de cada parcela agrícola para restablecer sus límites; para solventar eso, los egipcios inventaron la geometría, según Heródoto.1
El modo de calcular el área de un polígono como la suma de las áreas de los triángulos, es un método que fue propuesto por primera vez por el sabio griego Antifón hacia el año 430 a. C. Hallar el área de una figura curva entraña más dificultad. El método de agotamiento consiste en inscribir y circunscribir polígonos en la figura geométrica, aumentar el número de lados de dichos polígonos y hallar el área buscada. Con el sistema que se conoce como método exhaustivo de Eudoxo, consiguió obtener una aproximación para calcular el área de un círculo. Dicho sistema fue empleado tiempo después por Arquímedes para resolver otros problemas similares,2 así como el cálculo aproximado del número π.
Área de figuras planas[editar]
Área de un triángulo
El área de un triángulo es igual al semiproducto entre la longitud de una base y la altura relativa a esta:3
- donde b es la base del triángulo y h es la altura correspondiente a la base. (se puede considerar cualquier lado como base)
- Si el triángulo es rectángulo, la altura coincide con uno de los catetos, con lo cual el área es igual al semiproducto de los catetos:

- donde a y b son los catetos.
- Si se conoce la longitud de sus lados, se puede aplicar la fórmula de Herón.
- donde a, b, c son los valores de las longitudes de sus lados, s = ½ (a + b + c) es el semiperimetro del triángulo.
- Si el triángulo es equilátero, el área es igual a un cuarto del cuadrado de un lado por la raíz cuadrada de 3:
- donde a es un lado del triángulo.
Área de un cuadrilátero
El área del trapezoide o de cualquier cuadrilátero es igual al semiproducto de sus diagonales por el seno del ángulo que forman.
- El área también se puede obtener mediante triangulación:
- Siendo:
 el ángulo comprendido entre los lados
el ángulo comprendido entre los lados  y
y  .
. el ángulo comprendido entre los lados
el ángulo comprendido entre los lados  y
y  .
.
- El rectángulo es un paralelogramo cuyos ángulos son todos de 90º, y el área es igual al producto de dos de sus lados contiguos a y b:3
- El rombo es un paralelogramo, cuyos 4 lados son iguales, y tiene su área dada por el semiproducto de sus dos diagonales:
- El cuadrado es el polígono regular de cuatro lados; es a la vez un rectángulo y un rombo, por lo que su área puede ser calculada de la misma manera que la de estos dos. En particular, dado que sus lados son iguales, se usa la fórmula:3
- El trapecio, el cual tiene dos lados opuestos paralelos entre sí y dos lados no paralelos, tiene un área que viene dada por la media aritmética de sus lados paralelos multiplicado por la distancia entre ellos (altura):3
Área del círculo y la elipse[editar]
El área de un círculo, o la delimitada por una circunferencia, se calcula mediante la siguiente expresión matemática:4
Área delimitada entre dos funciones[editar]
Una forma para hallar el área delimitada entre dos funciones, es utilizando el cálculo integral:
El resultado de esta integral es el área comprendida entre las curvas:  y
y ![g(x) [< f(x)]\,](http://upload.wikimedia.org/math/1/d/3/1d3507ab25c5f1c6f1f965b2397293c3.png) en el intervalo
en el intervalo ![[a,b]\,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) .
.
 y
y ![g(x) [< f(x)]\,](http://upload.wikimedia.org/math/1/d/3/1d3507ab25c5f1c6f1f965b2397293c3.png) en el intervalo
en el intervalo ![[a,b]\,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) .
.- Ejemplo
Si se quiere hallar el área delimitada entre el eje x y la función  en el intervalo
en el intervalo ![[-2;2]](http://upload.wikimedia.org/math/6/1/5/615951c7c4b124cb26541f3feb881b2b.png) , se utiliza la ecuación anterior, en este caso:
, se utiliza la ecuación anterior, en este caso:  entonces evaluando la integral, se obtiene:
entonces evaluando la integral, se obtiene:
 en el intervalo
en el intervalo ![[-2;2]](http://upload.wikimedia.org/math/6/1/5/615951c7c4b124cb26541f3feb881b2b.png) , se utiliza la ecuación anterior, en este caso:
, se utiliza la ecuación anterior, en este caso:  entonces evaluando la integral, se obtiene:
entonces evaluando la integral, se obtiene:
Por lo que se concluye que el área delimitada es  .
.
 .
.
El volumen encerrado entre dos funciones también puede ser reducido al cálculo de una integral, similar.
Relación área-perímetro
Dada una curva simple cerrada en el plano euclídeo puede probarse que su longitud o perímetro del área encerrada y la propia área encerrada satisfacen la relación:
La igualdad se alcanza sólo para un círculo el resto de figuras y formas posibles cumplen la desigualdad estricta.
Área de superficies curvas
El área de una superficie curva es más complejo y en general supone realizar algún tipo de idealización o límite para medirlo.
- Cuando la superficie es desarrollable, como sucede con el área lateral de un cilindro o de un cono el área de la superficie puede calcularse a partir del área desarrollada que siempre es una figura plana. Unacondición matemática necesaria para que una superficie sea desarrollable es que su curvatura gaussiana sea nula.
- Cuando la superficie no es desarrollable, el cálculo de la superficie o la fórmula analítica para encontrar dicho valor es más trabajoso. Un ejemplo de superficie no desarrollable es la esfera ya que su curvatura gaussiana coincide con el inverso de su radio al cuadrado, y por tanto no es cero. Sin embargo la esfera es una superficie de revolución.
Superficie de revolución
Cuando una superficie curva puede ser generada haciendo girar un curva plana o generatriz alrededor de un eje directriz, la superficie resultante se llama superficie de revolución y su área puede ser calculada fácilmente a partir de la longitud de la curva generatriz que al girar conforma la superficie. Si y=f(x) es la ecuación que define un tramo de curva, al girar esta curva alrededor del eje X se genera una superficie de revolución cuya área lateral vale:
Ejemplos particulares de superficies de revolución son:
- El área de esfera de radio R que viene dada por
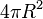
- El área de un cono de radio R y de altura h viene dada por
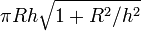
- El área lateral de un cilindro de radio R y altura h es simplemente
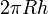
Cálculo general de áreas[editar]
Mediante la geometría diferencial de superficies o más generalmente la geometría riemanniana puede calcularse el área de cualquier superficie curva finita. Si la superficie viene dada por la función explícita z = f(x, y) entonces, dada una región Ω contenida en una superficie su área resultar ser:
De manera un poco más general si conocemos la ecuación paramétrica de la superficie en función de dos coordenadas cualesquiera u y v entonces el área anterior puede escribirse como:
Donde E, F y G son las componentes del tensor métrico o primera forma fundamental de la superficie en las coordenadas paramétricas u y v.
En una variedad de Riemann de dimensión n > 1 puede definirse el área de ciertas subvariedades cuya dimensión sea 2. Para ello se define un conjunto de dos coordenadas (u, v) que parametricen la subvariedad y se construye un atlas para subvariedad, entonces el área es la integral de una 2-forma sobre dicha variedad. Esta definición coincidiría con la definición de áreas dada a partir de la primera forma fundamental.
Webgrafìa:http://es.wikipedia.org/wiki/Wikipedia:Portada
Webgrafìa:http://es.wikipedia.org/wiki/Wikipedia:Portada
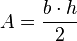
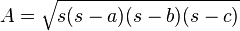
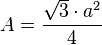







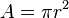


![\begin{array}{rl}
A(-2,2) & = \int^2_{-2} | 4 - x^2 - 0 | dx = 2 \int^2_0 4 - x^2 dx = \\
& = 2\left[4x - \cfrac{x^3}{3} \right]_0^2 = 2 \left[ 8 - \left(\cfrac{2^3 - 0}{3}\right) \right] = \cfrac{32}{3}
\end{array}](http://upload.wikimedia.org/math/1/5/1/151429a207a548ff127d3cab0849f7ef.png)












 viene dado por:
viene dado por:
 es la función característica de la región R:
es la función característica de la región R:
 :
: